For generations, how many vertices does a cube have, mathematicians and enthusiasts have been captivated by geometry, the study of forms and their characteristics. The cube is one of the most recognisable and basic three-dimensional shapes among all the geometric shapes. The exciting subject of how many vertices a cube has comes up frequently while we are exploring cubes. We shall dig into the intriguing realm of cubes and examine their vertice count in depth in this extensive blog.
Understanding the Cube:
A cube is a three-dimensional geometric shape that belongs to the prism class of polyhedrons. A cube is distinguished by the special mix of these features:
- Faces: There are six congruent, identical square faces on a cube. The arrangement of these faces results in right angles at their edges since they are perpendicular to one another.
- Edges: There are twelve equal edges on the cube. Each edge joins two vertices to produce a segment that encircles the square faces.
- Vertices: The main areas of interest for our investigation are these. Vertices are points or corners formed by the intersection of edges. A vertex, then, is the point at which three edges come together at a 90-degree angle.
How Many Vertices Does a Cube Have?
Let’s now address the main query: How many vertices are there in a cube?
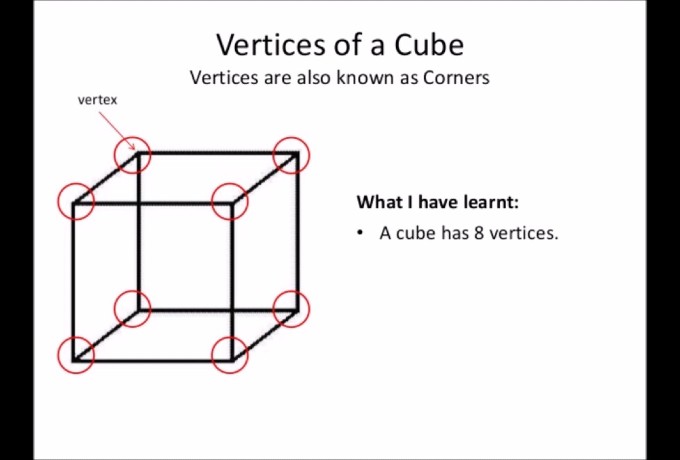
- Every Corner Is a Vertex: In a cube, a vertex is represented by each of the eight corners. These corners are unique locations where three edges converge to form a vertex that determines the cube’s form and structure.
- Distinctive Features: It’s important to how many vertices does a cube have remember that the cube has distinct vertices while having similar faces and edges. Every vertex has unique geometric features because it has a unique collection of adjacent faces and edges.
- Visualising the Vertices: To picture a cube’s vertices, picture a traditional six-sided die. The eight vertices of a cube are represented by the eight dots on the dice. Every dot represents one of the cube’s corners.
Ultimately, a cube has eight vertices in all. These vertices how many vertices does a cube have are essential for characterising the shape of the cube and are involved in many geometric and mathematical computations, transformations, and real-world uses.
Practical Applications:
Cubes have many real-world applications in a variety of industries; they are not only mathematical abstractions:
- Architecture: Cubic forms how many vertices does a cube have are frequently used by architects to create modern, minimalist constructions that highlight geometric simplicity.
- Engineering: To create accurate 3D models and prototypes, engineers utilise cubes. In civil engineering, cubes are crucial for planning buildings and other structures.
- Puzzles & Games: One of the best examples of how cubes may be used to amuse and test problem-solving abilities is the well-known Rubik’s Cube.
- Computer Graphics: Cubes are a basic feature in computer graphics and 3D modelling because vertices play a crucial role in creating the shape and structure of things.
Conclusion
With its eight vertices, the cube how many vertices does a cube have is a fundamental unit of geometrical analysis. Knowing a cube’s characteristics and its vertices is crucial for anybody working in architecture, engineering, design, or mathematics. The fact that it is not just a mathematical idea but also a how many vertices does a cube have necessary component of more intricate constructions and designs shows how important geometry is to our daily lives.